Ada Lovelace 
- Saw true potential: beyond arithmetic
- Programmed Bernoulli numbers → tedious by hand, feasible by Engine
- Challenge: algorithms had to be fully explicit
- Ada had to:
- Translate algorithm into machine-level detail
- Explain clearly to others
- Later: Turing gave formal foundations
- Debate continues: how revolutionary was this step?
Programs 
- From here: programs & programming
- Program = algorithm detailed for a machine
- Programming = creating programs
- Programming is hard, requires languages
- BUT: programs are a poor way to communicate algorithms to people
- Hard to read, especially large ones
- Raises questions:
- What counts as “explaining”?
- What does it mean to “understand”? (links to AI & philosophy)
Programs → Flowcharts 
- Programs not ideal for humans → need another way
- Enter: flowcharts
Flowcharts 
- Graphical representation of algorithms
- Easier to read than raw code
- Use boxes, diamonds, arrows, and text
 |
|---|
Flowcharts (conventions)
- Conventions:
- Entry → start point
- Box → operation (read input, arithmetic, assign)
- Diamond → decision (yes/no branch)
- Lines → show flow, can carry conditions/data
 |
|---|
Flowcharts (operations)
- The box = operation
- Simple action: input, calculation, assignment
 |
|---|
Flowcharts (decisions)
- The diamond = decision
- Compare something → branch Yes/No
 |
|---|
Flowcharts (lines)
- Lines may include:
- Condition to be true for path
- Data passed along that path
 |
|---|
Flowcharts (styles & UML)
- Many conventions exist → all similar
- No one “right” layout → goal is communication
- Flowcharts can:
- Be docs, planning tools, or debugging aids
- Split large projects among teams
- UML (Unified Modeling Language) = flowchart’s more formal cousin
- Used in high-precision projects
Pseudocode 
- Closer to code but still human-readable
- Looks like code, won’t run
- Flexible, less standardized than flowcharts
- Example:
for i ← 1 to n do
read x
s ← s + x
output s
Pseudocode (examples) 
Informal
Read a, b, c
max ← a
If b > max then max ← b
If c > max then max ← c
Print max
Formal
input: n ≥ 0
output: n!
p ← 1
for i ← 2 to n do
p ← p · i
return p
Pseudocode vs Code 
- Ideally, pseudocode
code translation is straightforward
Pseudocode
for i ← 1 to n do
read x
s ← s + x
output s
Java
for (int i=0; i<n; i++) {
int x = sc.nextInt();
s = s + x;
}
System.out.println(s);
Pseudocode (guidelines) 
- Omit language-specific quirks
- Keep general, map to any language
- Adapt for audience (math-heavy vs general)
- Example:
Math-friendly:
input: a₁…aₙ
s ← 0
for i ← 1..n do
s ← s + aᵢ
output s
General audience:
Read a list of numbers
Add them up
Print the total
Big Ideas in Algorithms
Idea 1
- Imagine I pick a number between 1 and 100
.
- You can ask: “Is it higher or lower
”
If you guess randomly, it could take 100 tries.
Can you do better?
Idea
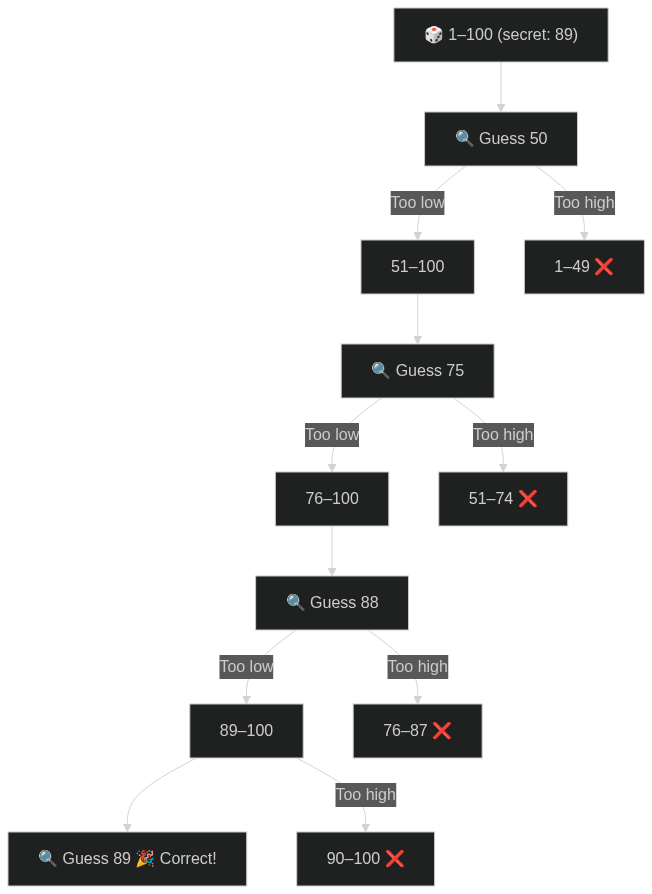
Binary Search
- Always guess the middle of the range.
- Each time, cut the possibilities in half.
- Find the secret number in just 7 tries.
 |
|---|
Why it matters ?
Binary Search
- Searching in a dictionary
- Finding songs in your playlist
- Quickly locating files on a laptop
- Finding players with similar rank in multiplayer games
Idea 2
Problem
- You have a pile of books all jumbled together.
- Goal: Put them in order (alphabetically by title).
- Sorting the whole pile at once is messy.
Idea
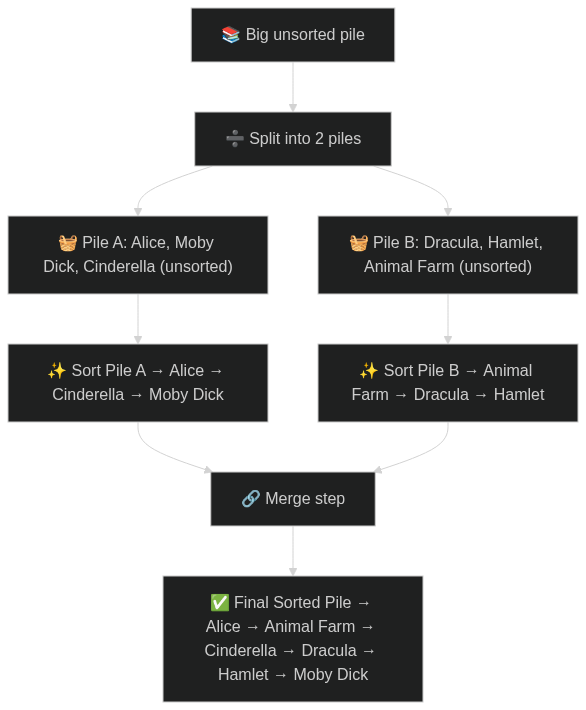
Merge Sort
- Split the pile into smaller piles.
- Sort each small pile individually (easy!).
- Merge piles
- Continue until you have one big, sorted pile.
 |
|---|
Why it matters
- Organizing playing cards
- Sorting names at graduation
- Sorting contacts on your phone
Idea 3
Problem
- A fire alarm rings in your ICS class (very unrealistic scenario).
- You want the closest exit.
- What’s the safest way to explore?
Idea
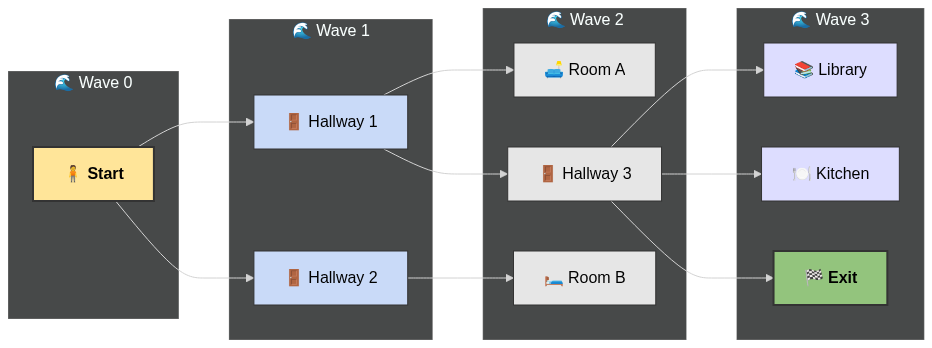
Breadth-First Search (BFS)
- Explore in waves:
- First check all rooms next to you.
- Then the rooms next to them.
- Keep going until you find the exit.
- Guarantees the shortest way out.
 |
|---|
Why it matters
- Social networks: “You and Sam are 3 steps apart”
- GPS: finding shortest bus routes
- Emergency drills: nearest exit
Idea 4
Problem
- You’re in a maze.
- You try one path → it’s a dead end.
- What do you do?
Idea
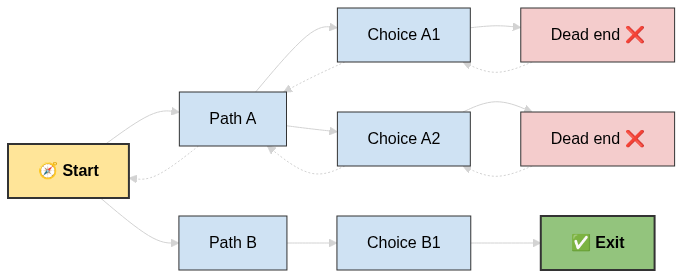
Backtracking
- Explore one path as far as possible.
- If blocked → step back.
- Try another path until you succeed.
 |
|---|
Why it matters
- Solving Sudoku
- Escape rooms
- Crossword puzzles
AutocomplainAutocomplete
Idea 5
Problem
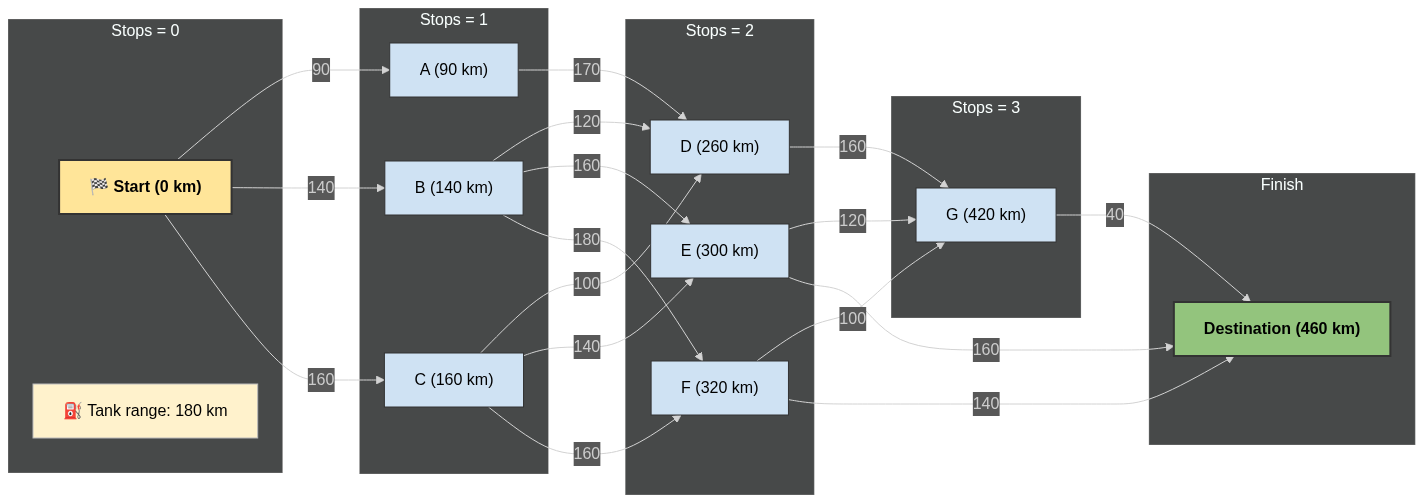
- You’re planning a road trip across Europe
.
- You want to stop for gas as few times as possible.
- There are many stations, but you can only drive a limited distance per tank.
- How do you plan?
Idea
Dynamic Programming
- Think of smaller trips first:
- Best way to drive 100 km.
- Then 200 km.
- Then 300 km.
- Reuse these answers to plan the full trip.
Build up the solution step by step.
 |
|---|
Why it matters
- Travel planning
- Budget optimization
- Scheduling projects
- DNA/protein analysis
Idea 6
Problem
You’re playing a dice game.
- The math is messy.
How can you find your chances of winning?
Idea
Monte Carlo
- Play the game many times.
- Count how often you win.
- Probability = wins ÷ trials.
Why it matters
- Casinos & gambling
- Predicting weather
- Stock market risks
- Movie recommendations
Idea 7
- You search “best pizza near me”
.
- Thousands of results.
- How does Google decide who’s first?
Idea
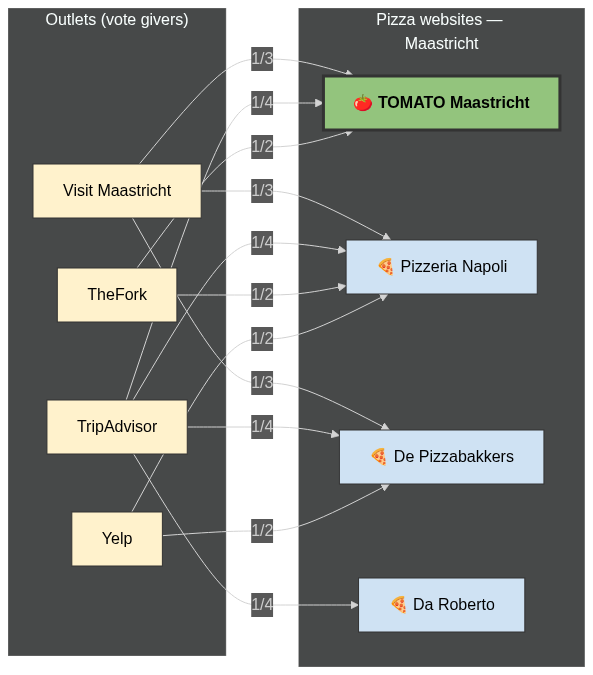
PageRank
- Each website votes by linking to others.
- Votes from popular sites count more.
- Pages with most “authority” rise to the top.
 |
|---|
Why it matters
- Search engines
- Instagram influencers
- Academic paper citations
What we learned 
- Binary Search: halve the problem each time.
- Merge Sort: divide work, then combine.
- BFS: ripple out to find shortest path.
- Backtracking: try → undo → try again.
- Dynamic Programming: build answers from smaller ones.
- Monte Carlo: use randomness to estimate.
- PageRank: trust flows through links.






























